수학의 신 초등수학 5-1(2026)은 2022 개정 교육과정에 맞춘 상위권 심화 문제 해결서로, 5학년 1학기 범위를 고난도까지 끌어올리도록 설계된 교재입니다. 책 앞부분에 단원별 핵심 개념과 확장 개념, 상위권 문제 비법을 한데 모아 예열 학습이 쉬우며, 자리가 많아 풀이 과정을 넉넉히 적고 점검하기에 충분합니다. 난이도 표기가 ‘어려움’으로 안내되어 있어 기본서 이후 응용·심화를 본격적으로 진행하려는 학습자에게 적합하다고 판단됩니다. 현재 미출간이지만 공개된 구성 정보를 기준으로 학습 가치를 평가하였습니다. 아래 수학의신 초5-1 답지를 첨부해두도록 하겠습니다. 표지를 꼭 확인하시길 바랍니다.

문항 구성은 대표 심화 문제를 Check→Practice→Master→Challenge의 4단계로 점층화하여 같은 개념을 소재 변경, 조건 변형·추가를 통해 반복 노출합니다. 이 구조는 ‘개념 확인→기본 응용→변형 대응→최상위 도전’의 흐름을 자연스럽게 유도하며, 조건 해석력과 전략 선택, 검산 습관까지 함께 잡을 수 있게 돕습니다. 해설은 정답 제시를 넘어 핵심 관문을 짚어 주는 방식이라 다양한 풀이를 비교하며 사고 폭을 넓히기에 유리합니다. 단원 말의 마무리 세트는 시험 친화적 구성이어서 속도와 정확도를 동시에 훈련하기 좋습니다. 아래 링크를 통해 수학의 신 5-1 답지를 열람할 수 있습니다.
학습 범위는 ‘자연수의 혼합 계산, 약수와 배수, 대응 관계, 약분과 통분, 분수의 덧셈·뺄셈, 다각형의 둘레와 넓이’로 구성됩니다. 연산 단원에서는 우선순위와 괄호 처리, 어림·검산을 요구하는 문장제가 다수 배치되어 연산의 정확도와 해석력을 함께 강화합니다. 약수·배수와 분수 단원은 공약수·공배수 개념을 바탕으로 약분·통분을 체계화해 분수 연산의 발목을 잡는 병목을 해소하는 데 도움이 됩니다. ‘대응 관계’는 함수적 관점을 싹틔우는 연결 고리이며, 도형 단원은 공식 암기를 넘어 분할·합성과 단위 변환을 활용해 넓이 개념을 확장하도록 유도합니다.
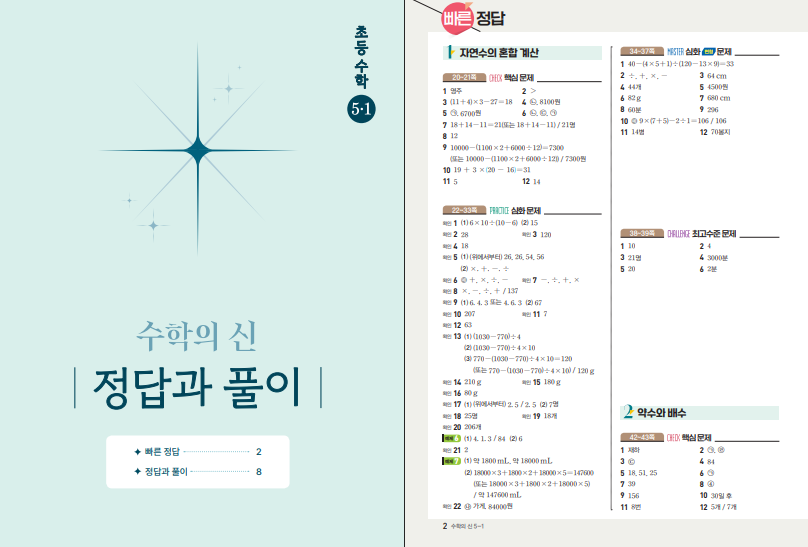
활용법은 개념서 1회독 이후 주 3회, 회당 40~50분 루틴을 권합니다. 1주 차에는 Check 전량으로 약점을 진단하고, 2~3주 차에 Practice→Master를 완주한 뒤 주말에 Challenge로 난도 적응을 하시면 효과적입니다. 오답 정리는 ‘틀린 이유–놓친 조건–대체 전략’ 세 줄만 간단히 남기고 24시간 내 재풀이하면 학습 유지율이 높습니다. 현재 출간 일정이 연기된 상태이므로, 출간 전까지는 연계 단원(혼합 계산, 약수·배수, 분수 기본)을 별도의 기본서·드릴로 예열해 두면 본 교재 학습 전환이 매끄럽겠습니다. 총평하자면, 본서는 1학기 심화·변형 대비와 상위권 도약을 동시에 노리는 학습자에게 신뢰할 만한 선택지입니다. 본문에 22개정 수학의 신 초5-1 답지를 pdf 파일로 첨부해두었습니다.